Multi Armed Bandit 변천사 훑어보기

30 minute read

특정 컨텐츠에 순위를 매긴다는 개념은 IR 분야에서 Learning to Rank 프레임워크로 많이 연구가 되었습니다. 최근 랭킹 트렌드는 그 경계가 모호해진 것 같고, 실시간 학습/인퍼런스 보다는 딥러닝 모델과 같이 배치 학습/인퍼런스가 이루어지는 경우가 많은 것 같지만, 추천 분야에서는 Online Learning의 필요성이 많았고, Online Learning to Rank를 MAB 프레임워크로 풀어나가는 경우가 여전히 많습니다.

MAB 프레임워크로 OLTR을 어떻게 정의하는지와, 그 변천사를 간략히 정리해보았습니다.

언급된 MAB 알고리즘

기존 Classical MAB : $\epsilon$-greedy, UCB, Thompson Sampling

Contextual MAB : LinUCB (WWW 10), LinTS (ICML 13), GIRO (ICML 19)

Non-stationary MAB : DiscountedUCB + SlidingWindowUCB (ALT 11), CUSUM-UCB + PHT-UCB (AAAI 18), dTS (NIPS 17)

Contextual + Non-stationary MAB : NeuralBandit (ICONIP 14), dLinUCB (SIGIR 18)

Multiple Play MAB

단순 해결 : MP-TS + IMP-TS (ICML 15)
Click Model과 결합 : CascadeUCB1 + CascadeKL-UCB (ICML 15), RecurRank(ICML 19)-Non MAB
Combinatorial 관점: CUCB (ICML 13)
Combinatorial + Volatile arm : CC-MAB (NIPS 18)

Batched Update MAB : bTS (IEEE BigData 18)

Using Feedback as Relative Perspective : RUCB (ICML 14), CDB (RecSys 19)

Exploration-Exploitation Dilemma

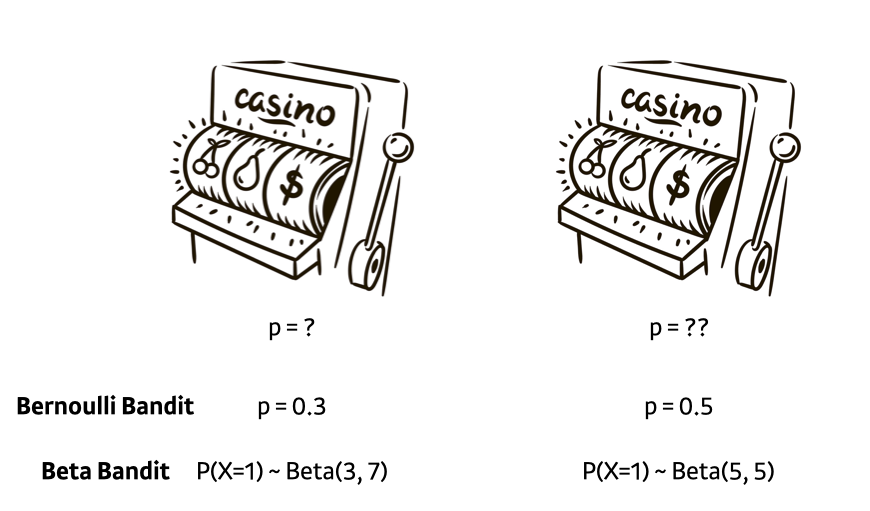
외팔이 강도가 2개의 슬롯머신을 당길 기회가 있는데, 두 개의 슬롯머신은 reward를 반환할 확률이 다르다고 합시다. 그걸 모르는 상태에서 어떻게 슬롯 머신을 당겨야 가장 높은 reward 기댓값을 얻을 수 있을까요?

Classical MAB에서 사용하는 가정은 일반적으로 슬롯머신이 reward를 반환할 확률이 베르누이 분포를 따른다고 가정합니다. 그렇다면 둘 중에 확률이 높은 슬롯머신만 계속 당긴다면 최고의 결과를 얻을 수 있을 것입니다. 하지만, 우리는 oracle (확률 또는 분포를 알고 있는 절대자)이 아니기 때문에 일단 당겨보면서 어떤 슬롯머신이 더 많은 reward를 반환할지 탐험을 해야할 필요가 있습니다.

여기서, 최선의 선택 (그림에서는 오른쪽 슬롯머신)을 했을 때의 reward 기댓값, 그리고 최선의 선택을 하지 않았을 때의 reward 기댓값의 차이를 regret이라고 합니다. 위 그림을 예시로 들면 왼쪽 머신을 당길 때마다 0.2의 regret이 누적되는 것입니다. regret을 정의하는 방법은 논문마다 다르기도 하지만, 실서비스 적용에서 그리 중요한 포인트는 아니기 때문에 컨셉만 알고 넘어가면 될 것 같습니다.

그렇다면, 추천 시스템에서는 reward를 어떻게 정의할까요? 노출 (impression) 후 click이 발생한 경우 reward 1이 발생, unclick이 발생한 경우는 reward가 발생하지 않는다고 정의하면, reward의 기댓값은 노출대비 클릭의 기댓값이 되고, 그리고 그건 CTR이 됩니다!! Tada~~ 그렇기 때문에 regret 최소화 == CTR 최대화와 동일해집니다.

요약하면: 모르지만, 당겨보면서 알아가보자

Classical MAB

1. $e$-greedy

트래픽 중, $\epsilon$ 만큼의 비율은 무작위로 탐색(exploration)하고, 나머지 $1-\epsilon$ 에 대해 지금까지 관찰된 결과를 바탕으로 탐욕적으로 가장 최선의 arm을 draw하는 (empirical) 전략을 $\epsilon$-greedy 전략이라 부릅니다. 시도마다 슬롯 손잡이 $a$ 의 reward의 기댓값 (CTR)을 추정해 나가고, 시도가 계속될 수록 reward의 추정치는 참값에 수렴함을 가정합니다. 하지만, 관측 횟수가 적은 경우에는 관측결과의 신뢰도가 매우 낮기 때문에 문제가 생깁니다. (ex. 12345를 4번 추천했는데 3이 2번 4가 1번 실제로 클릭되었다. 그러면 3이 best case일까? 이 결과를 믿을 수 있을까?) 반대로, 관측 횟수가 충분히 많아 신뢰도가 높은데도 $\epsilon$ 만큼의 explore를 반드시 해야한다는 점이 문제가 됩니다. 이러한 문제를 시간의 흐름 (시도 횟수)에 따라 $\epsilon$ 값을 적절하게 감소시켜가며 해결할 수도 있습니다. 적절하게 탐색 확률을 감소시킨다면 T시점에 최선의 선택을 하지 않는데서 발생하는 Regret $R_A(T)$를 T로 나눈 값, $R_A(T)/T$ 는 0에 수렴하게 됩니다.

2. Optimism in Face of Uncertainty (OFU)

OFU는 불확실한 것을 낙관적으로 보자는 컨셉의 알고리즘입니다. ~~투자를 하고난 직후에는 장밋빛 미래가 그려지는 것 처럼~~

앞서 설명한 $\epsilon$-greedy는 항상 empirical mean이 좋은 arm만을 고르고, 나머지를 입실론의 확률로 고르지만, 실제 arm에서 얻는 보상은 constant가 아닌 특정 분포에서 draw되는 r.v라고 보는 것이 합리적이기 때문에 탐색 전략에 신뢰구간의 개념을 도입합니다. OFU는 현재까지 관찰된 결과를 바탕으로 통계적으로 계산된 신뢰구간의 상한선 (Upper Confidence Bound) 를 그 arm의 가치로 보고, 그 arm을 draw 합니다.

예를 들어, 관찰된 결과를 바탕으로 아래와 같은 사후분포를 추정해 냈을 때, 누가봐도 평균값은 파란색<초록색<주황색 순서이지만, 95% 신뢰구간의 상한선은 파란색이 제일 높으므로, 파란색 arm을 draw하는 것입니다.

UCB를 정의하는 방법에 따라 여러 변형 알고리즘들이 있지만, 대표적인 UCB 알고리즘인 UCB1이 arm을 고르는 방식은 다음과 같습니다.

\[i = \underset{i}{argmax} \bar{x_i}+\sqrt{\frac{2lnt}{n_i}}\]

$x_i$ 는 i번째 arm의 지금까지 관측한 reward (클릭)의 평균값이고, $n_i$ 는 arm i가 play (impression)된 횟수를 의미합니다. 위의 값은 arm i의 실제 보상에 대한 $1-\frac{1}{t}$ 의 신뢰구간의 upper bound를 의미하는 것으로, Chernoff-Hoeffding bound 에 의해 얻어지는 값입니다. 처음에는 관측 결과 수가 적은 arm들이 뽑힐 확률이 높지만 (exploration), time은 log scale로 증가, $n_i$ 는 linear하게 증가하므로 우항의 값은 시간이 흐를 수록 작아지고, exploration의 비율이 시간이 흐름에 따라 감소합니다.

3. Thompson Sampling

Probability Matching이라고도 불립니다. Google Analytics의 AB 테스팅 최적화에도 사용된 알고리즘이며, 일반적으로 UCB나 $\epsilon$-greedy 보다 성능이 높음이 보여져있습니다. 시간 t마다 정책에 따라 arm a를 선택하고, 그에 상응하는 reward $r$ 을 받을 때, Thompson sampling은 관측치 ($a_t,r_t$) 와 파라미터 $\theta$ 를 사용해 likelihood function $P(r \mid a, \theta)$ 를 설계한 다음, prior를 가정해 MAP (Maximum A Posteriori)를 푸는 것입니다. 이 때, 각각의 arm의 reward가 관찰될 확률 $\theta_k$이 독립적인 베르누이 분포를 따른다고 가정했을 때, conjugacy 특성으로 인해 prior를 베타분포로 잡는다면, posterior 또한 베타분포가 됩니다. 이 때, $\theta_k$ 는 다음과 같은 파라미터를 가집니다.

\[\theta_k \sim Beta(\alpha_k, \beta_k)\]

분포가 가정되었기 때문에 분포를 통해 평균과 분산을 알 수 있습니다. 이 때, 분산이 의미하는 것은 Explore 입니다. 베타 분포의 평균과 분산은 다음과 같은 모양입니다.

\[\begin{align} E[\theta_k] &= \frac{\alpha}{\alpha+\beta} \newline V[\theta_k] &= \frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)} \end{align}\]

Thompson Sampling의 파라미터 업데이트는 다음과 같이 이루어지기 때문에, 시행이 거듭될 수록 분산은 작아지게 되므로, Exploration의 정도는 줄어들게 됩니다. 이 때, $c_i \in {0, 1}$ 는 클릭의 유무를 의미합니다.

\[\begin{align} p(u) &\propto \mu^{\alpha-1}(1-\mu)^{\beta-1} \; \newline Likelihood &= \prod_{i=1}^N \mu^{x_i}(1-\mu)^{1-x_i} \newline posterior &= likelihood \cdot prior \end{align}\]

OFU 알고리즘은 추정된 분포의 신뢰구간 상한선을 바탕으로 의사결정을 했다면, TS 알고리즘은 추정된 분포로부터 직접 샘플을 뽑아 의사결정을 합니다.

아래 영상은 베르누이 밴딧에서 Thompson Sampling을 구현하여 시뮬레이션 한 것입니다. 각 밴딧에서 reward가 관찰될 확률이 $\theta=[0.1,0.2,0.3,0.4]$ 인 $K=4$ 인 밴딧 상황에서 베타분포가 적합되는 과정을 관찰할 수 있습니다. 동시에, Exploration-Exploitation의 정도도 관찰할 수 있습니다.

After Classical

하나의 논문을 정독하기보다는 MAB 연구의 추세를 폭넓게 이해해보고자 하였습니다.

MAB 리서치를 진행하며 느낀점은, sota 논문들은 대부분 기존 MAB 방법론들을 베이스라인으로 실험을 진행하고, 그 것들보다 성능이 나음을 주장하고 있다는 점입니다. 그러나, 대부분의 MAB 논문들이 stationary, Top-1 draw, reward ~ R-sub gaussian 등 이상적인 상황을 가정하고 있기 때문에 sota 알고리즘을 소개하는 논문에서의 성능 향상, 특히 offline evaluation 상황은 실 서비스에 적용했을 때 성능향상이 실제로 일어날지 최대한 의심하며, sota 알고리즘이 기존의 알고리즘에서 극복하려고 한 한계는 무엇인가? 를 중심으로 리서치를 진행했습니다. 여러 알고리즘들의 컨셉을 잘 정리해두면 후일에 더 빠른 문제해결에 도움이 될 것이라고 생각하기 때문입니다.

1. Non-stationary MAB

Classical MAB에서 reward distribution이 time-independent하다는 가정을 파괴합니다. 시간이 흐르면 특정 arm의 CTR 기댓값은 감소하거나 증가할 수 있다는 것입니다. Non-stationary 환경은 서서히 reward의 기댓값이 변한다는 Slowly-varying, breakpoint 전후에는 일정함을 유지한다는 Abrubtly-changing 두 가지로 구분되어 정의되고, 이러한 각각의 환경에 맞게 MAB policy 또한 크게 두가지 범주로 나누어 집니다.

1.1. Passively Adaptive Policies

시간 할인의 개념을 이용해 최근 데이터에 높은 가중치를 줌으로써 현재 의 best arm을 찾습니다. 이 범주에 속하는 ofu 방법으로는 DiscountedUCB, SlidingWindowUCB 가 있고, 톰슨 샘플링 기반으로는 Taming Non-stationary Bandits: A Bayesian Approach (NIPS 2017) 에서 소개된 _discounted Thompson Sampling (dTS)_가 있습니다.

_DiscountedUCB_는 지난 관측 결과일수록 gamma를 이용해 시간할인을 하여 그 영향력을 감소시키며, _SlidingWindowUCB_는 지정된 윈도우 기간만큼의 관측 결과만을 사용합니다. 이러한 수동적인 적응 방법론은 과거의 데이터의 영향력을 줄이는 것이지 사용하지 않는 것이 아니기 때문에 급격한 변화에 발빠르게 대응을 하지 못하는 Time-lag 문제가 발생합니다.

1.2. Actively Adaptive Policies

급격한 변화를 빠르게 잡아낼 수 있는 Change Detection Algorithm을 사용합니다. Two-sided CUSUM UCB, PHT-UCB가 A Change-Detection based Framework for Piecewise-stationary MAB Problem (AAAI 2018) 에서 소개되었습니다. 이 중 Two-sided CUSUM UCB는 Fault Detection을 위해 주로 사용하는 통계적 관리도 (SPC) 변화 탐지 모형 중 누적합을 이용한 CUSUM 관리도를 이용한 것이고, PHT-UCB 는 Page-Hinkley Test를 이용해 변화 탐지를 하는 모형입니다.

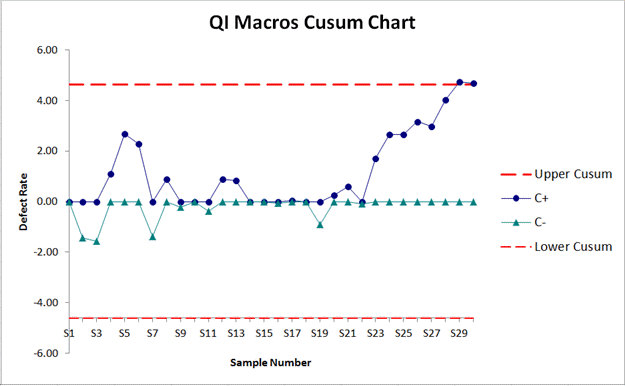
모형이 CUSUM 또는 PHT Chart의 UCB나 LCB에 변화 탐지 신호를 보내는 경우 bandit algorithm을 리셋하여 재학습을 진행합니다. 그 구조는 다음과 같습니다.

contextual bandit 상황에서의 non-stationary 환경을 고려한 알고리즘은 A Neural Networks Committee for the Contextual Bandit Problem (ICONIP 2014)에서 소개된 NeuralBandit, Learning Contextual Bandits in a Non-stationary Environment (SIGIR 2018)에서 소개된 dLinUCB가 있습니다.

dLinUCB 알고리즘은 여러 개의 slave bandit model을 동시에 업데이트하며, reward의 신뢰구간을 바탕으로 낡은 모델을 폐기하고 재학습시키며 현재 최적의 model을 사용하는 독특한 방식을 사용하는데 slave model들이 LinUCB 한 종류여야 할 필요가 없기 때문에 여러 모델을 앙상블하여 사용할 수 있는 독특한 구조를 제안합니다.

2. Context-Reward Relationship

슬롯머신이야 reward가 관찰될 확률이 고정되어 있지만, 실제 서비스에서는 reward가 관찰될 확률이 주변 환경이나 사용자에 따라 변할 수 있습니다. 그렇다면, reward의 분포가 컨텍스트와 무관하게 Bernoulli 분포를 따른다고 가정하는 것 또한 치명적인 문제가 생깁니다.

그래서 기존 MAB 스키마에서 사용하고 있지 않던 정보인 context와 feedback feedback을 결합해 reward의 분포를 학습하는데 반영하는 시도가 contextual bandits 을 통해 이루어졌습니다. LinTS와 LinUCB는 user(query), content의 context와 reward의 기댓값이 선형 관계를 가짐을 가정함으로써 feedback 뿐만 아니라 context 정보를 이용해 reward의 기댓값을 학습하는데 사용합니다. 또한, 두 알고리즘 모두 SGD 등의 방식을 사용하지 않고 Closed Form으로 ridge regression 파라미터를 업데이트합니다.

하지만, context와 reward의 기댓값은 선형관계라는 LinTS와 LinUCB의 기본 가정에 의문을 제기할 수도 있습니다. NNBandit (ICONIP 2014) 은 Neural Net이 Universal approximator임을 이용하여 context와 reward의 기댓값 사이의 non-linear한 관계를 표현하는 모델입니다.

이외에도, GLM, Balanced linear model, Adaptive learning, Bootstrap 등의 해결책도 제시가 되었습니다. 모델이 복잡할 수록 context-reward 관계를 잘 잡아내는 것은 당연하나, 이 연산이 bandit들의 모든 arm에 대해 이루어져야 하기 때문에 조금이라도 연산량이 많아지면 실 실행시간이 가장 크게 증가할 여력이 있는 부분이고, linear form 이 아닌 경우 online learning 상황에서 closed form이 아닌 SGD, Mini-Batch 방식의 업데이트를 수행해야 하기 때문에 연산량과 가용자원을 고려해서 반드시 상황에 맞는 모델을 선택해야 합니다.

3. Multi-play

Multi-armed bandit의 multi는 arm이 K개 있다는 것을 가정하지만, 한 번에 1개의 arm만 당길 수 있는 single play 상황을 가정합니다. 하지만, 실서비스에서는 문어가 K arms 들 중 한 개만 draw하는 것이 아닌 여러 개를 한꺼번에 draw를 해야하는 경우도 분명 존재합니다.

~~L개를 동시에 당기려니 헷갈리나보다~~

1개만 draw (impression)을 했을 경우 이 추천결과를 click한다면 1, 아니면 0의 reward 값을 주는데, 여러 개 (best L)을 한꺼번에 draw하는 경우에도 같은 방법으로 reward를 업데이트하는 것이 reasonable한지 의문을 가질 필요가 있습니다. 왜냐하면, 각 arm에서 독립적으로 $\theta_k$ 의 확률로 reward가 관찰되는 것이 아닌, 최대 1번의 reward가 관찰된다는 제약이 있기 때문입니다.

3.1 Simple Idea

Optimal Regret Analysis of Thompson Sampling in Stochastic MAB Problem with Multiple Plays (ICML 2015) 에서 multi-play 상황에 대처하는 방식을 소개하고 있습니다. 해당 논문에서 제안된 MP-TS는 사실상 TS와 큰 차이가 없는데, multiple-play 상황에서 Beta draw를 실시하여 top-1이 아닌 스코어 순으로 top-L개를 draw하고, 1 또는 0의 reward를 업데이트 합니다.

동시에, MP-TS의 개선 버전으로 I(mproved)MP-TS를 제안하는데, suboptimal draw가 너무 많이 일어나니 L개의 slot 중 L-1개에는 기존 관찰 결과로부터 최선의 결과를 (exploitation), 1개에서만 기존 Thompson sampling의 Beta draw를 실시(Exploration)한다는 것입니다.

위 방법은, L개의 draw된 모든 arm들이 독립적인 Expectation reward을 가지고 있다는 가정하에는 합리적이지만, 현실은 그렇지 않습니다. L개의 노출 컨텐츠 중, n번째의 컨텐츠를 클릭한 유저 중에는 n+1번째부터의 노출 컨텐츠는 쳐다보지도 않은 사람이 있을 수도 있고, 3번째 노출 컨텐츠가 4번째 노출 컨텐츠 클릭에 영향을 줄 수도 있습니다. 또한, L개가 모두 마음에 들었어도 클릭은 최대 한 개만 할 수 있습니다.

3.2 Click Model

이러한 연구는 IR 분야에서 유저의 행동 패턴을 분석하는 Click Model과 MAB를 결합하여 해결하려는 시도로 이어졌는데, 대표적인 Click Model은 다음과 같습니다. (참고 : Click Models for Web Search (Authors’ version))

Notation

$u$ : document id

$q$ : user’s query

$u_r$ : A document at rank r

$C_u$ : r.v for Click document u

$E_u$ : r.v for Examinate document u

$A_u$ : r.v for Attractiveness of document u

$S_r$ : r.v for Satisfaction level after click

Random Click Model (RCM)

\[P(C_u = 1) = \rho\]

가장 기본이 되는 CTR 예측 모델로 모든 컨텐츠 u는 동일한 클릭 확률 $\rho$ 를 가지고 있다고 가정하는 모델입니다. Classical MAB는 해당 모델을 기본 가정으로 하고 있습니다.

Rank-Based CTR Model (RCTR)

\[P(C_r = 1) = \rho_r\]

컨텐츠가 노출된 순서(rank)에 따라 CTR의 기댓값이 달라진다고 가정하는 모델입니다. RCM보다는 상당히 현실적인 베이스라인 모델인데, Accurately interpreting clickthrough data as implicit feedback (SIGIR 2005) 의 유저 행동 패턴 연구에서 관측된 데이터에서도 Rank 1 컨텐츠의 CTR이 0.45인 것에 비해 Rank 10 컨텐츠의 CTR은 0.05보다 낮은 CTR 값을 보여줬고, 실제 사내 서비스의 클릭 모델도 위치에 따라 위 실험결과와 유사한 CTR을 보여줍니다.

다만, 이 Click ratio를 그대로 RCTR 모형에 적용을 할 수는 없는 것이, 실제 슬롯별 CTR은 rank의 효과에만 영향을 받는 것이 아닌, MAB가 최선의 rank를 찾기 위한 노력의 효과에도 같이 영향을 받기 때문입니다.

Position-based Model (PBM)

PBM의 CTR은 위와같은 Bayesian Network(참고 : PRML-Bayesian Network)로 나타낼 수 있습니다. 이 모형은 유저 q가 추천 컨텐츠를 확인(Examine)함과 동시에 해당 컨텐츠에 이끌려야 (Attracted) 클릭이 일어난다는 모형입니다. 해당 모형에서 검사 여부와 이끌림 여부는 독립이라고 가정하며, 검사 여부는 컨텐츠 u의 rank에 영향을 받고, 이끌림 여부는 유저 q와 컨텐츠 u에 동시에 영향을 받는다고 가정합니다. 따라서 위의 베이즈 네트워크는 아래와 같은 수식으로 표현됩니다.

\[\begin{align} P(C_u=1)&=P(E_u=1)\cdot P(A_u=1) \newline P(A_u=1) &= \alpha_{uq} \newline P(E_u=1)&=\gamma_{r_u} \end{align}\]

Cascade Model (CM)

An experimental comparison of click position-bias models (WSDM 2008) 에서 소개된 가장 널리쓰이는 유저 행동패턴 가정으로, 유저가 컨텐츠를 top-to-bottom으로 원하는(relevant) 컨텐츠를 찾을 때까지 계속 스크롤한다는 것입니다. 이를 나타내는 베이즈 네트워크는 아래와 같습니다.

CM 모델에서는 1번째 추천 컨텐츠는 항상 검토(examined)되며, r번째 컨텐츠는 r-1번째 컨텐츠가 검토되고 동시에 클릭되지 않아야만 검토됩니다. 그 수식은 다음과 같습니다.

\[\begin{align} C_r=1 &\leftrightarrow E_r = 1 \; and \; A_r=1 \newline P(A_r=1) &= \alpha_{u_rq} \newline P(E_1=1) &= 1 \newline P(E_r=1 | E_{r-1}=0) &= 0 \newline P(E_r=1 | C_{r-1}=1) &= 0 \newline P(E_r=1 | E_{r-1}=1, C_{r-1}=0) &= 1 \end{align}\]

이외에도 DCM 등 다양한 클릭 모델들이 존재합니다.

이러한 클릭 모델은 슬롯별 CTR 예측에 사용되는데, 해당 모델들이 Eye Tracking 등 HCI 기반의 연구와 함께 이루어져 실제 유저의 행동패턴을 잘 반영한다는 특성때문에 클릭 모델과 MAB를 결합하려는 시도가 Cascading Bandits: Learning to Rank in the Cascade Model (ICML 2015) 에서 이루어지게 됩니다. 이는 Click Model 중 가장 널리쓰이는 Cascade model과 MAB를 결합한 것이며, 논문에 CascadeUCB1, CascadeKL-UCB가 소개되어 있습니다.

또한 위에서 언급한 IMP-TS를 소개한 논문 Appendix에 Cascade 상황에서 생기는 bias를 해결하기 위해 MP-TS를 변형한 BC-MP-TS (Bias-Corrected MP TS)또한 소개됩니다.

해당 모델에 contextual 버전을 추가한 CascadeLinTS, CascadeLinUCB는 Cascading Bandits for Large-Scale Recommendation Problems (UAI 2016)에 소개되었습니다.

3.3 Combinatorial Bandit

Combinatorial bandit 은 클릭 모델을 이용하는 것보다 더 폭 넓은 관점의 bandit 알고리즘입니다.

이 밴딧 알고리즘의 활발한 후속 연구를 이끈 논문은 Combinatorial MAB: General Framework, Results and Applications (ICML 2013) 입니다. Cascade Bandit은 Vertical 방식으로 추천결과가 나열되면서, 같은 추천 결과에서 여러 번의 클릭이 일어날 수 있는 IR 분야에 적합한 밴딧 알고리즘이라고 한다면 Combinatorial 방식은 Super arm의 개념을 도입해 조금 더 범용적이고, 추천시스템에 적합한 multiple-draw 상황의 전략을 도출해냅니다.

여러 개의 arm을 draw해야 하는 상황에서, arm끼리 상관관계도 있어 개별 arm의 절대적 가치를 추정하는 것의 정당성이 흔들리니, 함께 draw 하는 arm의 조합을 super arm으로 정의하는 것입니다.

가장 단순하게 생각한다면, 존재할 수 있는 모든 super arm을 각각의 arm처럼 다룬다면 기존 Classical 1-draw bandit 방식으로 문제를 풀 수 있습니다. 하지만, arm이 $m$개 존재한다면 존재 가능한 super arm은 최대 $2^m$ 개, L개를 draw하는 상황에서는 $_mC_L$개로 기존 arm의 개수보다 exponential 하게 증가하기 때문에 이러한 방식으로 문제를 풀어나갈 수는 없습니다.

그렇기 때문에, 위 논문에서는 적절한 arm들의 조합을 구성하기 위한 oracle 함수를 만들 것을 제안합니다. oracle 함수는 논문마다 그 방식이 다르지만, 지금까지 관찰된 arm들의 draw와 reward 데이터를 바탕으로 개별 arm (underlying arm)들의 Expectation vector를 구성해 이 벡터를 바탕으로 최적의 arm의 조합인 super arm을 구성해주는 함수입니다. 어떻게 매핑을 하냐가 가장 중요한 부분인데, 위 논문에서는 $\alpha,\beta$-Approximation 을 통해 super arm을 구성하고, Efficient Ordered Combinatorial Semi-Bandits for Whole-Page Recommendation (AAAI 2017)에서는 Oracle 대신 Maximization 문제를 정의하고, 이를 integer programming으로 푸는 대신 연산 효율을 위해 다음과 같은 구조의 네트워크로 계산합니다.

Combinatorial Bandit을 늦게 공부하기 시작해 더 정리하지 못한 점이 아쉬운데, Contextual Combinatorial MAB with Volatile Arms and Submodular Reward (NIPS 2018)는 사용 가능한 arm의 풀이 지속적으로 변하는 (volatile arms) 상황을 고려한 combinatorial bandit 알고리즘인 CC-MAB 를 소개합니다.

4. Batched Update

A Batched Multi-Armed Bandit Approach to News Headline Testing (IEEE BigData 2018) 야후 리서치에서 이루어진 연구입니다. MAB는 arm을 draw하는 것과 reward를 업데이트 하는 것이 이벤트 단위로 순차적으로 바로 일어난다고 가정하고 있는데, 실제 서비스에서는 트래픽이 매우 빠른 속도로 들어와 batch 단위로 일어날 수 밖에 없는 상황을 고려한 bTS (batched Thompson Sampling) 알고리즘을 제안합니다.

해당 논문에서는 베타분포의 파라미터를 업데이트 하는 방법을 summation과 normalization을 제안했는데, normalization 업데이트 방식은 배치 단위로 트래픽이 쏠림으로서 발생하는 부작용을 해결하고자 제안된 방법입니다.

[Summation] $c_t$ : 배치 t의 click, $u_t$ : 배치 t의 unclick

\[\begin{align} \alpha_{t+1} &= \alpha_{t} + c_t \newline \beta_{t+1} &= \beta_{t} +u_t \end{align}\]

[Normalization] $M_t$ : t 배치에서 해당 밴딧의 모든 arm들의 impression 수, $K$ : arm의 수

\[\begin{align} \alpha_{t+1} &= \alpha_{t} + \frac{M_t}{K}\frac{c_t}{c_t + u_t} \newline \beta_{t+1} &= \beta_{t} + \frac{M_t}{K}\left ( 1 - \frac{c_t}{c_t+u_t} \right ) \end{align}\]

그러나, 해당 논문에서의 실험 결과는 summation 방식이 훨씬 좋은 성능을 보였는데 저자들은 normalization update를 하면서 발생하는 noise의 효과가 side-effect를 처리하는 효과보다 큰 것 같다고 분석했습니다.

5. Arm의 가치는 절대적인가? (OLTR)

이번엔 조금 큰 틀에서의 문제 제기입니다. Top L from N 문제에서 MAB의 기본 가정은 arm마다 절대적인 가치가 있다는 것입니다. (reward의 기댓값), 해당 가정을 이용하지 않는 방식으로 Online Learning to Rank (OLTR) 문제를 풀어나가는 방법 또한 간략히 조사해보았습니다.

Learning to Rank는 IR 분야에 뿌리를 두고 있습니다. 추천 시스템에서는 MAB 방식의 online learning 방식이 널리 사용되고는 있지만, IR 분야에서는 다른 방식과 MAB 방식의 learning to rank를 다음의 논문에서 비교한 적이 있었습니다. Online Learning to Rank : Absolute vs Relative (WWW 2015)

Absolute 접근법은 일반적인 contextual bandit을 의미하는 것으로, document context, query, user context로부터 정보를 종합해 context features를 구성하고 이를 이용해 유저 피드백 데이터의 절대적 가치 (MAB 방식에서는 reward의 기댓값인 CTR)을 추정해 나가는 접근법입니다.

하지만, Relative 접근법은 특정 컨텐츠의 절대적 가치가 존재한다는 것에 자체에 대해 의문을 제기합니다. 여러 개의 추천 결과를 노출하는 상황에서 유저 피드백 데이터로부터 얻는 정보는 해당 컨텐츠의 절대적 가치라기 보다는 같이 노출된 컨텐츠들 간의 상대적 우위(relative preference)일 뿐이라고 생각하는 것입니다. 이러한 상대적 접근법에 해당하는 모델들은 유저 피드백을 Stochastic Gradient Descent 방식으로 업데이트 함으로써 랭킹을 학습합니다.

위 논문에서는 LinUCB를 변형한 Lin-$\epsilon$과 Candidate Preselection(CPS) Learning to Rank 알고리즘을 비교했는데, 적은 숫자의 유저 쿼리와 문서(arm)이 있는 경우, 그리고 피드백에 노이즈가 없는 경우에는 MAB 방법론이 더 좋은 성능을 보이나, 유저 피드백에 노이즈가 많은 경우나 pool의 범위가 넓은 경우에는 Relative 접근법 (LTR)이 더 좋은 성능을 보인다고 결론지었습니다.

이런 Relative 접근 방법을 Bandit 알고리즘과 결합하려는 시도도 있었는데 이 분야의 Bandit 알고리즘은 Dueling Bandit이라 합니다. Relative UCB for the K-Armed Dueling Bandit Problem (ICML 2014)에서는 Feedback으로 얻은 정보를 한 쌍의 arm으로 부터의 상대적 선호를 나타낸다는 relative 해석법을 결합한 RUCB 알고리즘을 소개하고 있고, Online Learning to Rank for Sequential Music Recommendation (RecSys 2019)에서는 CDB 알고리즘을 소개하고 있습니다.

LTR 분야가 너무 폭 넓은 분야라 더 자세히 조사하지는 못했는데, SIGIR 2016에서 튜토리얼로 진행된 Online LTR for Information Retrieval 자료가 IR 분야에서의 LTR, 특히 Online LTR에 대해 상세하게 다루고 있으니 읽어보시면 좋을 것 같습니다. 기회가 된다면 더 읽어보고 정리할 예정입니다.

우리는 정말 無에서 시작하는가?

Exploration, Exploitation 딜레마의 근본적인 가정은 우리가 실제 노출결과가 어찌될지 모르기 때문에 일단 노출시켜보면서 탐색하고 알아낸다는 것입니다. 그렇다면, 우리는 정말 노출결과가 어찌될지 전혀 모르는 상태로 시작하는 걸까요?

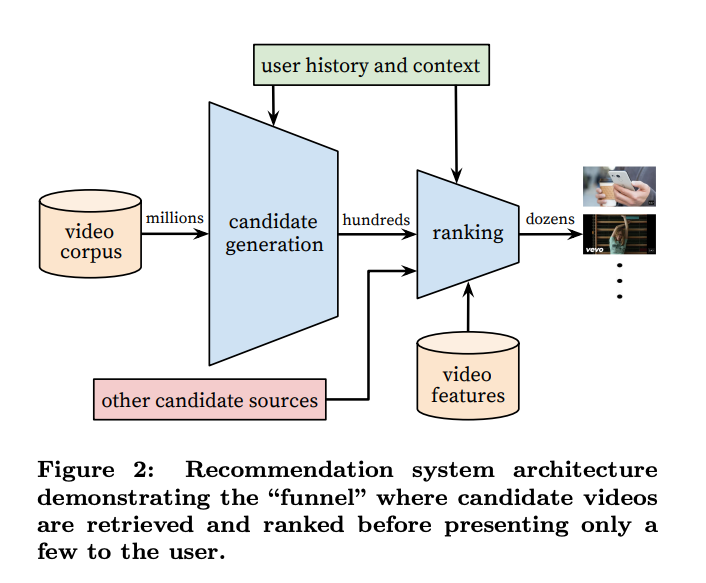
(출처: Deep Neural networks for YouTube Recommendations (Recsys 16))

일반적인 추천시스템 구조에서 Candidate Generation과 Ranking 사이에는 Scoring, Ensemble 단계가 있습니다 (이를 품질 평가 모델이라 부르기도 하는 것 같습니다). 해당 scoring이 online 상황에서의 reward가 상관계수가 높다면, 그냥 해당 score를 초기값처럼 사용할 수도 있습니다. 요즘은 사용할 수 있는 feature 또한 잘 정제가 되어있고, 모델이 계속 발전함에 따라 (deep! deeeeeep!) 조금 더 정밀한 사전 CTR Prediction이 가능하기 때문에, 오프라인 모델의 CTR 예측치를 MAB의 초기값으로 활용하는 방식으로 (ex. deep model의 컨텐츠 A에 대한 CTR 예측값이 0.1인 경우, Thompson Sampling의 컨텐츠 A에 대한 파라미터 초기값을 $\alpha=1$, $\beta=9$ 로 세팅한다.) MAB의 cold start 문제를 줄일 수도 있습니다.

Twitter Facebook LinkedIn

Jerry